STIRLING ENGINE
ME 200 Team 22
Preliminary Research
In the first discussion of our Heat Engine Project, we primarily identify how exactly a heat engine works and some basic calculations that are necessary to determine if a design is feasible or not. We first defined a heat engine or “pump”. Heat engines basically make use of the Vapor Compression Cycle, which works as follows: This cycle relies on evaporation and condensation to transfer heat across or against a temperature gradient. In the expansion process, the present fluid undergoes evaporation and leads to a lower temperature and pressure (refrigeration). Heat Engines make use of the condensation process by compression at constant entropy which superheats the present fluid and releases this heat for many different uses. Usually, this process requires a large amount of work to be done to cause this process.
The relative efficiencies of heat engines can be compared by calculating the Coefficient of Performance (CoP):
Stirling Engines
Fig. 1: The thermodynamic cycle of a Stirling Engine.
An ideal Stirling engine undergoes four thermodynamic processes per cycle. First, the gas expands isothermally by absorbing heat from a hot source (step 3-4). Then, the gas undergoes isochoric heat removal, causing the pressure to decrease (step 4-1). After, the gas contracts isothermally by rejecting heat into the cold sink (step 1-2). To complete the process, the gas undergoes isochoric heat addition, thereby raising the pressure and returning the system to its original state (step 2-3).
Efficiency of a Stirling Engine
The theoretical efficiency of an ideal Stirling engine depends on the temperature difference between its hot and cold ends. This value 𝜂 may be computed as follows:
This value is not achievable due to inefficiencies caused by friction between moving components of the engine, as well as heat lost via conduction. Additionally, heat provided by the candle cannot be entirely captured by the Stirling engine, further reducing its efficiency. The overall efficiency penalty multiplier 𝑛 needs to be experimentally determined.
Power of a Tea Candle
The heat generated by a tea light candle can be calculated using the equation:
Where m is mass, and u is the energy density of paraffin wax (42.0 kJ/g). The mass of a cylindrical candle can be found using the equation:
Where ρ is the density of paraffin wax, r is the radius of the candle, and h is the candle’s height. Using r = 1.9 cm, h = 1.27 cm, and ρ = 0.9 g/cm3, m becomes 13.03 g. Plugging this value into the equation for finding heat gives Q = 547 kJ. The power generated by the candle can be found using the equation:
Where Δt is the amount of time it takes for the candle to deplete its energy. Using Δt = 5 hours = 18000 seconds gives P = 30.4 W.
Work Required to Raise U.S. Quarters
We can compute the work required to raise and arbitrary 𝑘 U.S. quarters to 2 meters by the following equation:
Where m is the mass of a U.S. quarter (5.67 g), g is the gravity of the Earth (9.81 m/s2), and h is the raised height (2 m). We find that the work required to raise 𝑘 quarters is therefore 0.112∗𝑘 joules.
Simultaneously, the force produced by the Stirling engine must also be greater than the weight of the quarters.
The force exerted must be greater than 0.0557∗𝑘 Newtons.
Work Output of the Stirling Engine
To find the work output of the Stirling engine, the equation
Should be used for each process in the cycle. For the isochoric processes (process 2 and 4), W = 0 because there is no volume change. To calculate the work for the isothermal processes (process 1 and 3), substitute the equation of state for the pressure to give
Where R is the specific gas constant, which for air is 287 m2/(s2K), and m is the mass of the air. To find the mass of the air, assume that the gas that is trapped in the cylinder was at standard density (1.225 kg/m3) within a cylinder with r = 0.033 m and h = 0.114 m. Using the equations
With the specified values gives an air mass of 0.000478 kg. Assume that the compressed volume is 1% of the uncompressed volume. Assuming the transition from 2 to 3 and 4 to 1 lasts 0.1 seconds, the change in temperature between the two isothermal processes can be found using
Where CV is the volume-specific heat capacity of air (0.718 kJ/(kg K)) and P is the power of the candle. Evaluating the equation gives a temperature difference of 8.86 K. Assuming the isothermal contraction occurs at 293 K, the isothermal expansion then occurs at 301.86 K.
Now the work equation for an isothermal process can be evaluated as
For the isothermal expansion, , so . For the isothermal contraction, , so . Therefore, the net work, output by the engine is 5.60 J per cycle.
Coefficient of Performance (CoP)
Assuming the entire cycle lasts 0.5 seconds, the candle will provide a heat input of 15.2 J. Therefore, the coefficient of performance is 2.72. This is the ideal value because this analysis has not factored in any inefficiencies such as friction or that not all the candle’s heat is transferred to the air in the engine. In reality, the CoP will be higher than 2.72.


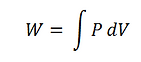
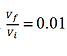
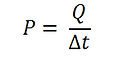
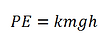
What does this all mean?
We've outlined all relevant parameters for our design challenge of eventually using the power generated from our engine to raise "k" number of quarters a distance of two meters off the ground. We've estimated the required amount of energy that can be produced by an average tea candle and we used this estimation to calculate the required efficiency for our engine. The more efficient our design is, the greater ability our engine will have in picking up the quarters.
We will keep these values in mind in the prototyping phase in an effort to increase the efficiency of our design as much as possible. This may be accomplished by reducing friction between each moving part, increasing the temperature differential (this translates to increased energy output), and reducing heat/fluid loss as much as possible (which ensures continuous power generation).
Where to next?
Our team examined the above types of Stirling Engine configurations before settling on the most practical design based on our price range and availability in materials. We settled on a design resembling that of the Beta Stirling Engine configuration due to its efficient use of space and material.
Our overall design process will pick up in the "Prototyping" section; where we walk through our iterations and concept refinement.