STIRLING ENGINE
ME 200 Team 22
Calculations and Analysis
Summary
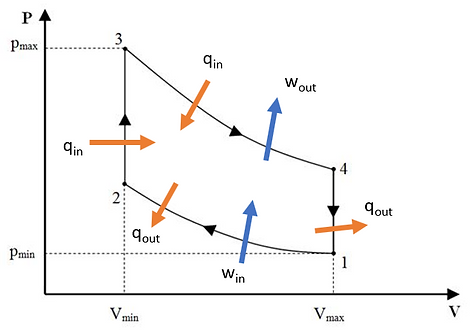
Figure 1: The pressure-volume diagram of the Stirling cycle.
The Stirling cycle shown in Figure 1 is a thermodynamic cycle that converts heat into work by using a change in temperature to drive a piston. The Stirling cycle is unique in that it can theoretically attain Carnot efficiency. In other words, for a given temperature range, it is the most efficient engine that can be constructed. The Stirling engine is able to do this because it contains an internal heat exchanger for capturing some of the heat that, for most engines, would be lost. This heat exchanger is also known as a regenerator.
The summary of the pressure, temperature, and enthalpy at each state point is included in Table 1. The temperatures were determined experimentally using an infrared sensor, and all other values were calculated.
Table 1: Summary of the variables at each state point.
The summary of the work and heat into and out of the system for each process in included in Table 2.
Table 2: Summary of the work and heat for each process.
Theses Tables indicate that under ideal conditions, the engine should produce 16.7 kJ/kg of specific net work from a net input of 16.7 kJ/kg of specific heat. When multiplied by the mass of the air in the engine, the net work becomes 7.98 J per cycle. In reality, these values will not be correct because this analysis does not account for inefficiencies such as friction and that not all of the candle's heat will be transferred into the engine. The equations and solution process used to produce these values are included below.
Additionally, the Coefficient of Performance (CoP) can be calculated using the equation
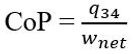
When the values from Table 2 are inserted into this equation, the CoP becomes 4.75. This is a measure of efficiency for an engine, with a number closer to 1 being more efficient.
Power of a Tea Candle
The heat generated by a tea light candle can be calculated using the equation
where m is mass, and u is the energy density of paraffin wax (42.0 kJ/g). The dimensions and density of the candle are r = 1.9 cm, h = 1.27 cm, and ρ = 0.9 g/cm^3. The mass of a cylindrical candle can be found using the equation
Plugging the mass into the equation for finding heat gives Q = 544.4 kJ. The power generated by the candle can be found using the following equation, where Δt is the amount of time it takes for the candle to deplete its energy:
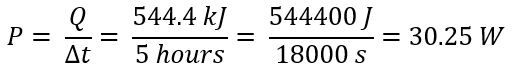
Work Required to Raise Quarters
We can compute the work required to raise and arbitrary k U.S. quarters to 2 meters by the equation
Where m is the mass of a U.S. quarter (5.67 g), g is the gravity of the Earth (9.81 m/s^2), and h is the raised height (2 m). We find that the work required to raise quarters is therefore 0.112k joules.
Simultaneously, the force produced by the Stirling engine must also be greater than the weight of the quarters.
The force exerted must be greater than 0.0557k Newtons.
Work Output of the Stirling Engine
To analyze the Stirling cycle, the temperature difference must be known, and to find the temperature difference, the mass of the air must be known. To find the mass of the air, assume that the gas that is trapped in the cylinder was at standard density (1.225 kg/m^3) within a cylinder with r = 0.033 m and h = 0.114 m. Using the equation
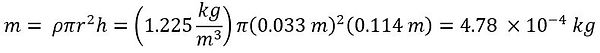
The change in temperature was found experimentally using an infrared sensor. Figure 2 shows the measurements (in Celsius).


Figure 2: The temperature measurements of the cold side (left) and hot side (right).
The initial specific volume can be found using
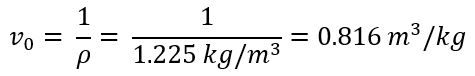
The compressed specific volume is assumed to be 50% of this value for this analysis.
Now each process can be evaluated. For the constant-volume processes (2-3 and 4-1), w = 0 kJ/kg, and the heat transferred in each constant-volume process is given by the First Law of Thermodynamics
For each constant-temperature process (1-2 and 3-4), there is no change in internal energy, so the First Law can be simplified to
To find the specific enthalpy at each state, use the Ideal Gas Properties of Air Table and interpolate based on the temperature of the state. To find the pressure at each state, apply the Ideal Gas Law:

The net work can then be calculated using
When the calculated values are substituted into this equation, the net work is 7.98 J per cycle.
What does this all mean?
In accordance with our preliminary research we find the energy required to raise "k" quarters to a height of 2 meters. We also find out how much energy our engine would output if working ideally solely based on the difference in temperature. If we had a friction less working design it would provide enough energy to lift approximately 71 quarters per cycle. Even if we consider non ideal conditions with friction, based on our difference in temperature we would've been able to raise some quarters to 2 meters. This was possible because of our high temperature difference that we achieved after adding the insulating layer of cardboard in our second prototype.
Where to next?
That's it! We've come a long way from simply understanding the basics of a Stirling Engine. Now, we have the ability to apply it in the real world. Who knows where this concept will end up in 5, 10, 20 years. It's up to students like us to decide. Thank you for your time!